Serie | Interaktive Datenvisualisierung – Einführung in Boxplots am Beispiel mit R
BI-Tools bieten eine große Vielfalt an Visualisierungen und zahlreiche Funktionen, um sie anzupassen. Doch bei dieser großen Auswahl stellen sich oft zwei Fragen: Welche Visualisierung ist die beste Visualisierung für meine Daten? Welche Art von Daten lassen sich am besten mit dieser Art von Visualisierung darstellen? In diesem Impuls lernen wir die Grundlagen einer der bekanntesten und am häufigsten benutzten Visualisierung kennen, nämlich den Box-Plot. Wir werden lernen, was man unter einem Box-Plot versteht, wie es zu interpretieren ist, und wie man mit den Grenzen dieser Visualisierung umgehen kann.
Definition Boxplot
Die Darstellung von Daten ist eine Gratwanderung zwischen der Vermittlung von Informationen und der visuellen Attraktivität und Verständlichkeit für das Publikum. Es ist daher unerlässlich, die Grundlagen bestimmter Darstellungen zu kennen, die aufgrund ihrer Robustheit und Korrektheit zu Recht sehr häufig verwendet werden. Eine dieser Darstellungen ist der Box-Plot, der in den 1970er Jahren von John Tukey entwickelt wurde. Wahrscheinlich haben Sie schon einmal einen Box-Plot gesehen, aber wissen Sie genau, wie es zu interpretieren ist? Schauen wir uns die Definition genauer an.
Für welche Daten sind Box-Plots geeignet?
Box-Plot sind für numerischen Datensätze, die ordinal geordnet sind. Was bedeutet es ? Nehmen wir ein Beispiel: Die Größe oder das Gewicht einer Person ist numerisch und kann viele Werte annehmen. In diesem Fall sind Box-Plots die richtige Art der Darstellung. Es ist wichtig zu wissen, dass die Verteilung der Daten nicht bekannt ist und uns im Moment nicht interessiert. Box-Plots können eine Möglichkeit sein, Daten zu untersuchen und etwas über die tatsächliche Verteilung der Daten zu erfahren. Die Daten können auch intervallkaliert (z.B. ein Gehalt: <20 000€, 20 000 – 40 000€, >40 000€) oder kategorisch (Rhesusgruppe A, B, AB und O) sein. Für diese Art von Daten ist der Box-Plot nicht geeignet und es sollten andere Darstellungen verwendet werden.
Anatomie eines Box-Plots
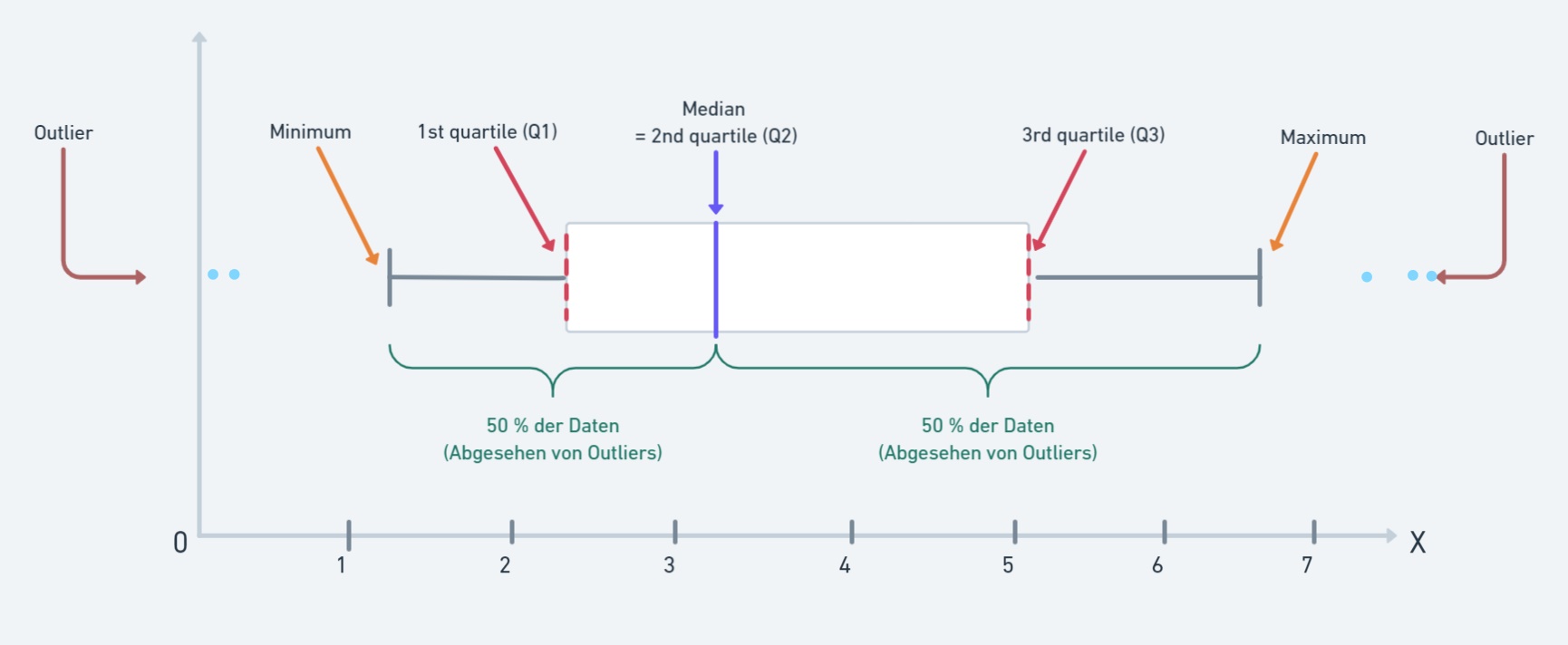
Wie sie im Bild sehen, entählt der Box-Plot viele Informationen! In der Mitte der Visualisierung befindet sich eine Box, die durch zwei Werte (Quartile) getrennt ist. Zusätzlich stellen die Extremwerte das Minimum und das Maximum dar. Insgesamt identifizieren wir fünf verschiedenen Merkmale:
- Minimum
- Maximum
- Median
- Erstes Quartil
- Drittes Quartil
Quartile
Der Box-Plot stellt die meisten Daten, die durch zwei Quartile (1. und 3.) getrennt sind, in einer Box dar. Quartile sind Schnittpunkte, die den Bereich einer Wahrscheinlichkeitsverteilung in kontinuierliche Intervalle mit gleichen Wahrscheinlichkeiten unterteilen, oder sie unterteilen die Beobachtungen in einer Stichprobe auf die gleiche Weise. Anders formuliert sind Quartile Werte, die sortierte Daten in vier Teile mit jeweils der gleichen Anzahl von Beobachtungen unterteilen.
- Erstes Quartil: Auch bekannt als Q1 oder das untere Quartil. Dies ist die Zahl, die in der Mitte zwischen der niedrigsten Zahl und der mittleren Zahl liegt.
- Drittes Quartil: Auch bekannt als Q3 oder das obere Quartil. Dies ist die Zahl, die in der Mitte zwischen der mittleren Zahl und der höchsten Zahl liegt.
Median
Der Median entspricht eingentlich dem zweiten Quartil: auch bekannt als Q2, eine Zahl, die auf halbem Weg zwischen der niedrigsten und der höchsten Zahl liegt. Die Definition unterscheidet sich geringfügig, wenn die Länge der Liste (die Anzahl der Elemente) gerade ist oder nicht.
Wenn
n
gerade ist:
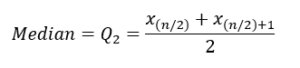
Wenn
n
ungerade ist:
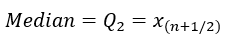
Extremwerte
Auf beiden Seiten dieser Box setzen wir zwei Markierungen, in der Regel das Maximum auf der einen und das Minimum auf der anderen Seite. Dies sind die whiskers (=Schnurrhaare) des Box-Plots. Manchmal ist die Verteilung der Daten sehr spärlich und wir verzichten darauf, das Maximum und Minimum zu markieren, sondern geben nur
![]()
ein. Der Interquartilsabstand ist wie folgt definiert:
![]()
Egal ob IQR oder Maximum/Minimum, der Rest der Werte, die so genannten Ausreißer, werden als einzelne Punkte in die Visualisierung eingefügt.
Praxis – Analyse an einem Beispiel
Für diesen Artikel verwenden wir einen bekannten Datensatz für die Analyse mit R: MT Cars. Der Datensatz ist ein integrierter Datensatz in R, der Messungen zu 11 verschiedenen Attributen für 32 verschiedene Autos enthält. Anschließend erstellen wir mit den Daten aus diesem Datensatz einfache Box-Plots, indem wir die Bibliothek ggplot2 verwenden.
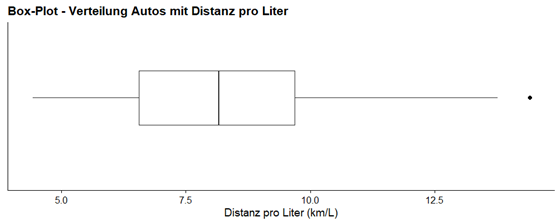
Wie wir sehen können, liegt der Median bei ca. 8 km/L und die Werte reichen von ca. 4 bis 13 km/L, mit einem Ausreißer bei etwa 14 km/L. Es ist sehr wichtig zu erwähnen, dass die y-Achse keine Skala hat und die Breite des Box-Plots absolut willkürlich ist. Ein Box-Plot kann auch auf der anderen Achse dargestellt werden und wird dann gespiegelt.
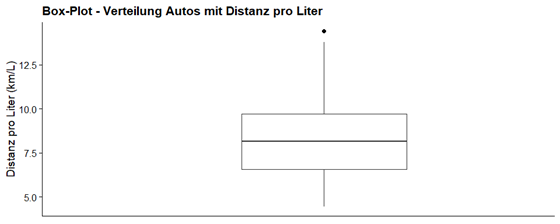
Wir identifizieren die gleichen Daten, aber der Box-Plot ist vertikal, was nur einen Unterschied in der Darstellung der Daten bedeutet, aber nichts an der Interpretation ändert. Es gibt noch die Möglichkeit, mehreren Box-Plots pro Visualisierung darzustellen. Da wir noch eine Axe ohne Daten haben, werden wir die Kategorien dort hinzugefügt.
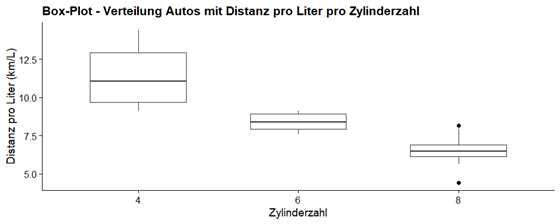
Wir stellen fest, dass je nach Zylinderkategorie der Median, das Maximum und das Minimum der Daten unterschiedlich sind. Wir können sogar eine ziemlich lineare Beziehung zwischen der Anzahl der Zylinder und der pro Kilometer zurückgelegten Strecke erkennen.
Einschränkungen
Sie sollten jedoch bedenken, dass die genaue Datenverteilung hinter jedem Box versteckt ist. Das bedeutet, dass die tatsächlichen Einzelwerte der Variablen nicht zu sehen sind. Einige Parameter, wie z. B. die Modalität der Verteilung, lassen sich mit dem Box-Plot nicht klar erkennen. Außerdem ist die Breite der einzelnen Box in keiner Weise genormt, sodass sie meist frei interpretiert werden kann, obwohl dies nicht der Fall sein sollte.
Erweiterungen
Es gibt jedoch einige Methoden, mit denen wir die Einschränkungen des Box-Plots überwinden können. Man kann einen Box-Plot mit der Darstellung der einzelnen Variablen auf derselben Achse (Dot plot) kombinieren.
## Bin width defaults to 1/30 of the range of the data. Pick better value with `binwidth`.
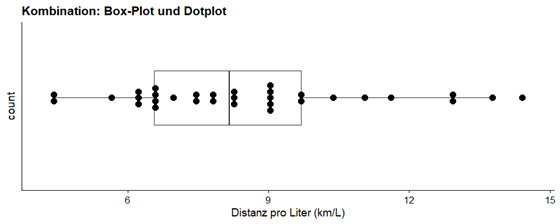
Hier ist deutlich zu erkennen, dass die Daten recht homogen verteilt sind.
Violinplots
Eine weitere Methode ist die Verwendung eines neuen Trends in der Datendarstellung: der Violinplot. Dieser Diagramtyp ermöglicht es, die Verteilung der Daten durch die Breite des Box-Plots (der bislang nicht verwendet wurde) zu sehen. Mit dem folgenden Beispiel kann man einen deutlichen Unterschied zwischen einer unimodalen und einer bimodalen Verteilung erkennen:
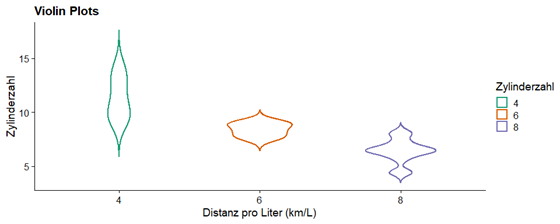
One more thing
Es ist auch möglich, Violinplots anders zu verwenden, d. h. die Breite des Plots beizubehalten, um die Verteilung zu beurteilen und gleichzeitig die verschiedenen Einzelwerte der Variablen zu visualisieren. Fügen wir alles zusammen, was wir gesehen haben!
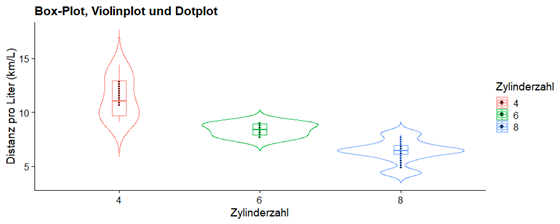
Dies war ein kleiner Überblick über Box-Plots, Violinplots und Dotplots mit R am Beispiel der MT Cars Daten. Kommen Sie auf uns zu, wenn Sie mehr zu statistischen Verfahren und die Möglichkeiten der Visualisierung erfahren möchten.
Interessiert? Dann nichts wie ab zu unserer Power BI Schulung, BI Einführungsworkshop oder Power BI Performanceoptimierung. Damit Wissen nicht nur theoretisch im Kopf bleibt, sondern praktisch umgesetzt werden kann.
Übersicht der interaktive Datenvisualisierung Serie:
- Datenbasierte Entscheidungen treffen und Handlungsempfehlungen aussprechen. Ein Fallbeispiel aus der Statistik zur Covid-19 Pandemie
- Einführung in Boxplots am Beispiel mit R
Haben wir Ihr Interesse geweckt? Kontaktieren Sie uns.
Ihre Ansprechpartner



