Serie | Data Science (ML & AI) – Architektur und Funktionsweise von baumartigen Regressionsverfahren
Entscheidungsbäume eignen sich als Machine Learning Modelle zur Lösung komplexer Klassifikations- und Regressionsprobleme. Zudem bilden Entscheidungsbäume die wesentliche Komponente von Random Forest und Gradient Boosting Verfahren.
Aufbau eines Regressionsbaums
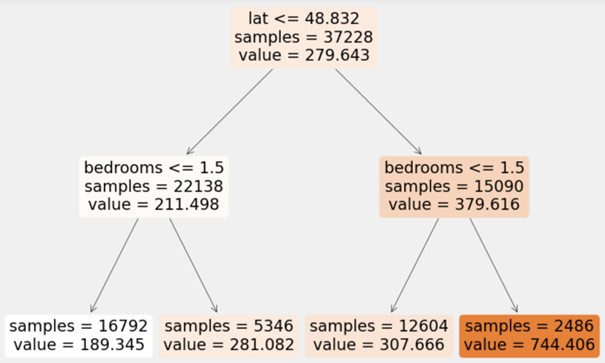
Der Wurzelknoten stellt den Beginn des Baums dar und repräsentiert den gesamten Datensatz. Von dort ausgehend wird der Datensatz durch die Nutzung eines einzelnen Features und eines Schwellwertes in zwei Partitionen aufgeteilt. In dem Beispiel unten zur Prädiktion von Preisen für Airbnb-Unterkünften ist das Kriterium zur Trennung des Datensatzes, ob der Breitengrad kleiner oder gleich 48,832 ist. Anschließend werden die beiden Teildatensätze weiter aufgeteilt, indem beispielsweise die 22.138 Unterkünfte mit einem Breitengrad von maximal 48,832 in zwei neue Partitionen eingeteilt werden, welche weniger oder mehr als 1,5 Schlafzimmer enthalten. Die Blätter des Baumes liefern schließlich die Vorhersage des Regressionsbaums. So wird zum Beispiel für Unterkünfte mit einem Breitengrad kleiner 48,832 und mehr als 1,5 Schlafzimmer ein Preis von 281,08€ prädiktiert.
Training eines Regressionsbaums
Zur Bestimmung eines Features und Schwellwertes für die Aufteilung des Datensatzes sucht der Algorithmus nach einem Kriterium, welches den geringsten Mean Squared Error (MSE) in den beiden erzeugten Teildatensätze gewichtet nach ihrer Größe produziert. Dazu versucht der Algorithmus folgende Kostenfunktion zu minimieren:
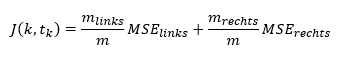
Dabei ist k das Feature, tk der Schwellwert, MSElinks/rechts der Mean Squared Error und mlinks/rechts die Anzahl der Einträge im linken/rechten Teildatensatz. Der Mean Squared Error beschreibt den Durchschnitt der quadrierten Abweichung zwischen den prädiktierten und tatsächlichen Werten. Die Aufteilung der Teildatensätze in weitere Partitionen erfolgt so lange, bis die maximale Baumtiefe erreicht ist oder keine Spaltung mehr gefunden wird, die zu einer Reduzierung des Mean Squared Errors führt.
Hyperparameter bei der Entwicklung eines Regressionsbaums
Mithilfe von Hyperparametern, wie der maximalen Baumtiefe, können Stoppbedingungen für die Aufteilung des Baumes in weitere Knoten definiert werden. Diese einschränkenden Parameter für die Struktur des Baumes dienen der Regularisierung und verhindern somit ein Overfitting des Modells. Overfitting beschreibt dabei eine Überanpassung des Modells an den Trainingssatz aufgrund einer zu hohen Modellkomplexität. Im Extremfall könnte ein nicht-parametrisierter Regressionsbaum beispielsweise einen derart großen Baum erzeugen, dass für jeden Eintrag des Trainingssatz genau ein Blatt mit dem entsprechenden Wert der Zielvariable erzeugt wird. Ein solcher Regressionsbaum würde zwar perfekte Vorhersagen auf dem Trainingssatz produzieren, jedoch wären diese Prädiktionen für den Testsatz unbrauchbar.
Neben der Festlegung der maximalen Baumtiefe, welche die Anzahl der Ebenen im Regressionsbaum beschränkt, kann die Struktur des Baumes auch durch andere Hyperparameter regularisiert werden. Dazu gehören die Angabe der Anzahl an Einträgen, die ein Knoten mindestens enthalten muss, bevor er aufgeteilt werden kann, und die Bestimmung der Anzahl an Einträgen, die ein Blattkonten mindestens beinhalten muss. Weitere Möglichkeiten sind die Festlegung der maximalen Anzahl an Blattknoten und der maximalen Anzahl an Features, welche zur Aufteilung eines Knotens ausgewertet werden.
Funktionsweise einer Random Forest Regression
Ein Problem von Entscheidungsbäumen besteht darin, dass sie sehr sensitiv gegenüber kleinen Veränderungen am Trainingssatz sind. Random Forests können diese Instabilität durch die Ermittlung einer durchschnittlichen Vorhersage mehrerer Bäume verringern. Diese Aggregation der Vorhersagen verschiedener Regressoren führt häufig zu einer besseren Prädiktion als die des besten individuellen Regressors. Eine solche Gruppe von Regressoren wird als Ensemble bezeichnet.
Eine Random Forest Regression besteht aus einer Menge von Regressionsbäumen, welche jeweils auf unterschiedlichen Teilen des Trainingssatzes trainiert werden. Um die Diversität der Bäume zusätzlich zu erhöhen, wird beim Training der einzelnen Regressionsbäume nur eine zufällige Teilmenge der Features für die Aufteilung jedes Knotens berücksichtigt. Zur Ermittlung einer Prädiktion der Random Forest Regression wird dann der Durchschnitt der Vorhersagen aller Regressionsbäume berechnet.
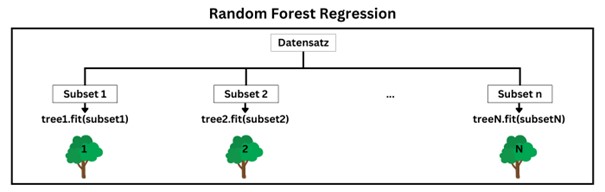
Hyperparameter einer Random Forest Regression
Der wichtigste Hyperparameter bei der Entwicklung einer Random Forest Regression ist die Anzahl der Regressionsbäume. Je höher die Anzahl der verwendeten Bäume ist, desto stärker werden die Vorteile der Ensemble Methode genutzt. Gleichzeitig steigt mit der zusätzlichen Modellkomplexität auch der Rechenaufwand für das Training sowie die Anwendung des Modells. Zusätzlich zur Baumanzahl stehen die gleichen Hyperparameter zur Regularisierung wie beim Training der individuellen Regressionsbäume zur Verfügung.
Architektur einer Gradient Boosting Regression
Gradient Boosting ist eine Weiterentwicklung von Random Forest. Der Ansatz bei der Gradient Boosting Regression besteht darin, die Regressionsbäume sequenziell zu trainieren und bei der Entwicklung jedes Baumes die Fehler des vorherigen Baumes zu korrigieren. Dazu wird ein neuer Regressionsbaum auf Basis der Residualfehler des vorherigen Regressionsbaums trainiert. Dadurch trifft der erste Baum eine Vorhersage für die Zielvariable, während der zweite Baum die Abweichung zwischen der Vorhersage des ersten Baums und dem tatsächlichen Wert der Zielvariable prädiktiert. Der dritte Baum schätzt dann die Differenz zwischen der vom zweiten Baum prädiktierten Abweichung und der tatsächlichen Abweichung. Bei der Anwendung der Gradient Boosting Regression zur Ermittlung einer Prädiktion werden somit die Vorhersagen aller Regressionsbäume im Ensemble aufsummiert.
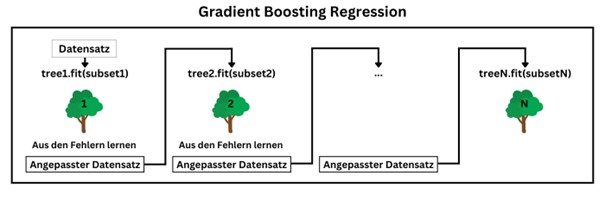
Hyperparameter einer Gradient Boosting Regression
Analog zur Random Forest Regression gibt es bei der Gradient Boosting Regression ebenfalls einen Hyperparameter für die Anzahl an Regressionsbäumen. Zudem können auch hier Hyperparameter zur Regularisierung, wie die maximale Baumtiefe, verwendet werden, um die Größe der einzelnen Regressionsbäume einzuschränken und Overfitting zu vermeiden.
Ein zusätzlicher Hyperparameter bei der Gradient Boosting Regression ist die Lernrate, welche den Beitrag der einzelnen Bäume skaliert. Dadurch ergibt sich ein Trade-off zwischen der Lernrate und der Anzahl an Regressionsbäumen. Bei einer geringen Lernrate werden mehr Bäume zur Anpassung des Modells an den Trainingssatz benötigt, aber die Prädiktionen generalisieren dafür besser auf dem Testsatz. Zur Ermittlung der optimalen Anzahl an Regressionsbäumen kann Early Stopping genutzt werden. Dabei wird der Vorhersagefehler des Modells nach jeder Erstellung eines neuen Baums während des Trainingsprozesses ausgewertet. Letztlich wird das Modell mit der optimalen Anzahl an Regressionsbäumen, welche zum geringsten Vorhersagefehler auf dem Validierungssatz geführt hat, neu trainiert.
Fazit
Baumartige Regressionsverfahren, wie Regressionsbäume, Random Forest und Gradient Boosting, sind leicht verständlich, interpretierbar, einfach und vielseitig einsetzbar sowie mächtige Vorhersagemodelle. Im Anschluss an die Beschreibung der Architektur und Funktionsweise von baumartigen Regressionsverfahren beschäftigt sich der nächste Teil mit der praktischen Anwendung, indem Modelle zur Prädiktion der Preise von Airbnb-Unterkünften entwickelt werden.
Übersicht der Data Science (ML & AI) Serie:
- AI im Fußball: Entwicklung eines Expected Goals Modells
- Einführung in Deep Learning und PyTorch
- NLP zur Analyse von E-Mails
- Entwicklung eines Machine Learning Modells auf Azure
- Architektur und Funktionsweise von neuronalen Netzen
- Entwicklung eines neuronalen Netzes zur Prädiktion von Airbnb-Preisen
- Architektur und Funktionsweise von baumartigen Regressionsverfahren
- Entwicklung baumartiger Regressionsverfahren zur Prädiktion von Airbnb-Preisen
- Large Language Models
- Das Large Language Model GPT-4
- Prompt Engineering in ChatGPT
- Entwicklung eines Large Language Modells mit LangChain & OpenAI
Haben wir Ihr Interesse geweckt? Kontaktieren Sie uns!
Ihr Ansprechpartner
