Serie | Data Science (ML & AI) – AI im Fußball: Entwicklung eines Expected Goals Modells

Die Nutzung von Daten im Fußball hat sich in den vergangenen Jahren stark entwickelt, weil durch den Einsatz von Sensortechnologien und verschiedenen Kameraperspektiven zu jedem Spiel eine große Menge an Daten gesammelt werden kann. Zudem erlangte der Einsatz von Datenanalysen im Sport durch das Buch sowie den Film Moneyball große Bekanntheit. Darin wird die Geschichte von Billy Beane erzählt, welcher in den 1990er-Jahren als Sportdirektor der Oakland Athletics trotz eines geringen Budgets eine erfolgreiche Baseball-Mannschaft durch die Nutzung von Daten aufbaute. Dabei verwendete Beane statistische Auswertungen zum Scouting von neuen Spielern, welche den finanzstärkeren Vereinen nicht aufgefallen sind. Dies inspirierte auch Vereine aus anderen Sportarten dazu, sich durch den Einsatz von Datenanalysen einen Wettbewerbsvorteil zu verschaffen. Im Fußball operieren beispielsweise der FC Midtjylland und der FC Brentford seit einigen Jahren nach dem Moneyball-System.

Eine Herausforderung bei der statistischen Auswertung von Fußballspielen liegt jedoch in der geringen Anzahl an Toren. Während in Sportarten wie Basketball oder Handball die Anzahl an Toren bereits ein starker Indikator für die Leistung einer Mannschaft oder eines Spielers ist, gewinnt im Fußball nicht automatisch die besser spielende Mannschaft und die Wichtigkeit eines Spielers lässt sich nicht zwingend an seiner Trefferanzahl erkennen.

An dieses Problem setzt das Expected Goals Modell an, welches für jeden Torschuss die Trefferwahrscheinlichkeit berechnet. Somit kann durch die Aufsummierung der Trefferwahrscheinlichkeiten aller Torschüsse die erwartete Anzahl an Toren ermittelt werden. Dies macht den Expected Goals Wert zu einem wesentlich besseren Indikator für die Qualität und Quantität der herausgespielten Torchancen als die Anzahl an erzielten Toren.

Das Expected Goals Modell hat sich in den letzten Jahren etabliert und wird unter anderem von Sky regelmäßig bei Bundesligaspielen eingeblendet. Doch wie ermittelt ein solches Modell die Trefferwahrscheinlichkeit eines Torschusses? Und welche Möglichkeiten ergeben sich durch die Nutzung des Modells bei der Leistungsbewertung von Mannschaften sowie beim Spielerscouting?

Entwicklung eines Expected Goals Modells mit künstlicher Intelligenz

Um die Trefferwahrscheinlichkeit eines Torschusses möglichst genau vorherzusagen, werden zunächst die Parameter identifiziert, welche die Trefferwahrscheinlichkeit positiv oder negativ beeinflussen. Anschließend werden diese Parameter als Input-Variablen für ein neuronales Netz genutzt, das mithilfe dieser Parameter die Trefferwahrscheinlichkeit für jeden Torschuss prädiktiert.

Verwendeter Datensatz

Als Datensatz wurde der frei verfügbare Datensatz von Statsbomb genutzt, welcher verschiedene Aktionen zu Fußballspielen enthält. Die Daten liegen als json-Dateien vor und beschreiben Aktionen wie Pässe, Schüsse, Zweikämpfe, Dribblings, Foulspiele oder Standardsituationen. Zum Beispiel enthält der Datensatz zu jedem Pass Informationen über den Passgeber und Empfänger, die Spielminute, Position, Höhe, Länge und Richtung eines Passes sowie vieles mehr.

Auswahl der Parameter zur Prädiktion der Trefferwahrscheinlichkeit

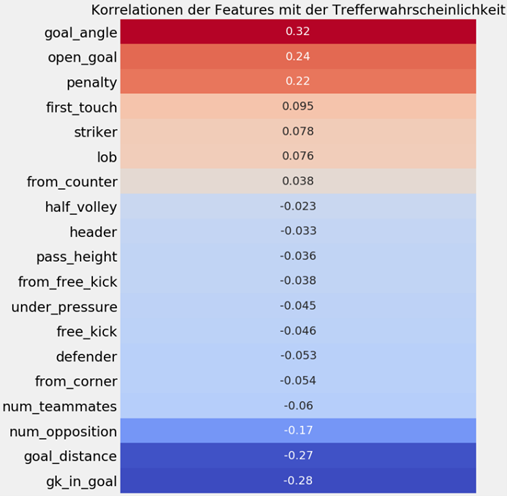
Zur Auswahl der Features wurde eine korrelationsbasierte Feature Selection durchgeführt. Dabei wurden zunächst in der Relevanzanalyse alle Features eliminiert, welche keine signifikante Korrelation zu der Zielvariablen aufweisen. Als Zielvariable dient hier eine binäre Variable, welche angibt, ob aus einem Torschuss ein Tor oder kein Tor resultierte. Anschließend wurden durch eine Redundanzanalyse alle redundanten Features eliminiert. Dazu wurde bei zwei stark miteinander korrelierenden Features das Feature eliminiert, welches schwächer mit der Zielvariablen korreliert. Insgesamt ergaben sich daraus 19 ausgewählte Features. Darunter befinden sich die kontinuierlichen Features zur Torentfernung, zum Schusswinkel sowie zur Anzahl an Mit- und Gegenspielern zwischen dem Schützen und dem Tor. Zusätzlich dazu gibt es 14 binäre Features und ein kategorisches Feature zur Höhe des Passes, welcher zum Torschuss führte. Dabei wird zwischen einem flachen, halbhohen und hohen Pass unterschieden.

Die Korrelationen der ausgewählten Features zur Zielvariablen werden in folgender Abbildung dargestellt. Dadurch veranschaulicht die Abbildung, wie stark sich die einzelnen Features positiv oder negativ auf die Trefferwahrscheinlichkeit eines Torschusses auswirken. Beispielsweise fällt auf, dass ein breiter Schusswinkel, ein leeres Tor und ein Elfmeter die Trefferwahrscheinlichkeit deutlich erhöhen. Gleichzeitig sinkt die Trefferwahrscheinlichkeit erheblich, wenn der Torhüter im Tor steht, die Torentfernung weit ist und sich viele Gegenspieler zwischen dem Schützen und dem Tor befinden.

Erstellung des Expected Goals Modells

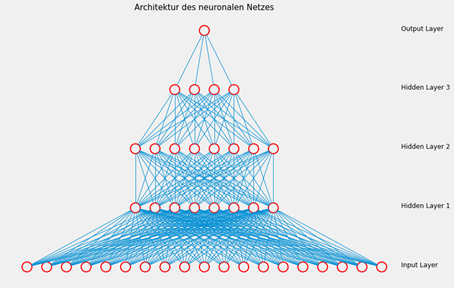
Zur Erstellung des Expected Goals Modells wurden alle 12.003 Torschüsse aus den 485 La-Liga-Spielen im Datensatz verwendet. Das Ziel besteht dabei in der Entwicklung eines Modells, welches mithilfe der ausgewählten Features als Input-Variablen einen möglichst genauen Wert für die Trefferwahrscheinlichkeit eines Torschusses prädiktiert. Dazu wurde ein neuronales Netz erstellt, welches aus insgesamt fünf Schichten besteht. Der Input Layer enthält die 19 Features und der Output Layer besteht aus einem Neuron für die Trefferwahrscheinlichkeit. Dazwischen liegen drei Hidden Layer, wobei die ersten beiden Schichten aus acht Neuronen bestehen und die letzte Hidden Layer vier Neuronen enthält.

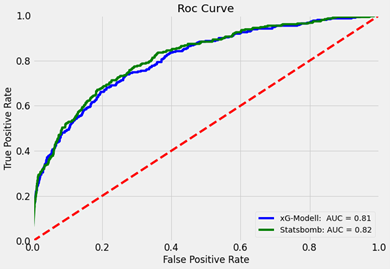
Als Kriterium zur Evaluation der Prädiktionen des neuronalen Netzes wurde der AUC-Wert verwendet, welcher die Fläche unter der ROC-Kurve bestimmt. Die ROC-Kurve beschreibt dabei das Verhältnis zwischen der True Positive Rate und der False Positive Rate. Dadurch drückt der AUC-Wert aus, wie hoch die Wahrscheinlichkeit ist, dass das Modell Torschüsse aus den beiden Klassen (Tor oder kein Tor) voneinander unterscheiden kann. Der AUC-Wert liegt zwischen null und eins, wobei ein höherer AUC-Wert ein genaueres Klassifikationsmodell indiziert.

Auf dem Testsatz liefert das trainierte neuronale Netz einen AUC-Wert von 0,81. Im Vergleich dazu liegt der AUC-Wert des Expected Goals Modells von Statsbomb, welches jedem Torschuss im Datensatz bereits eine Trefferwahrscheinlichkeit zugewiesen hat, bei 0,82 für diesen Testsatz. Die entsprechende ROC-Kurve der beiden Modelle wird unten graphisch dargestellt. Die rote, gestrichelte Line im Graphen symbolisiert ein zufälliges Modell, welches die beiden Klassen mit einer Wahrscheinlichkeit von 50% voneinander unterscheiden kann. Je besser das Modell ist, desto stärker nähert sich die ROC-Kurve dem Punkt in der linken, oberen Ecke bei (0;1) an. Die blaue ROC-Kurve des neuronalen Netzes verläuft dabei knapp unterhalb der grünen ROC-Kurve des Expected Goals Modells von StatsBomb.

Anwendungsmöglichkeiten des Modells

Spielerscouting

Das Expected Goals Modell kann unter anderem zum Scouting von Spielern eingesetzt werden. Dazu kann zum Beispiel für einzelne Spieler die erwartete Anzahl an Toren durch die Summe der Trefferwahrscheinlichkeiten aller Torschüsse des Spielers berechnet werden. Durch den Vergleich der erwarteten Anzahl an Toren mit der tatsächlichen Trefferanzahl können so Spieler identifiziert werden, welche eine besonders effiziente Chancenverwertung aufweisen. Auf diese Weise können beispielsweise Stürmer entdeckt werden, welche bei einem kleineren Verein trotz weniger Torchancen relativ viele Tore erzielen. Ein ähnliches Vorgehen kann auch angewendet werden, um mithilfe des Expected Goals Modells Mittelfeldspieler zu identifizieren, die durch ihr Passspiel besonders viele Torgelegenheiten kreieren. Durch den Vergleich der erwarteten Anzahl an Torvorlagen mit der realen Anzahl an Assists können Spieler gefunden werden, die eine hohe Anzahl an guten Torchancen herausspielen, aber trotzdem nicht groß auffallen, weil die Stürmer diese Tormöglichkeiten nicht effizient nutzen.

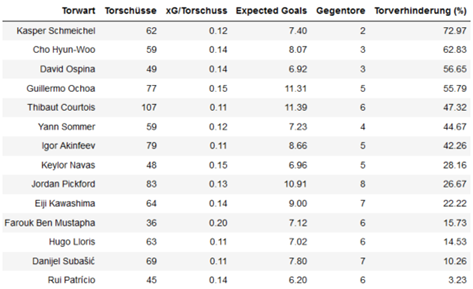
Zusätzlich zum Scouting von Feldspielern kann das Expected Goals Modell auch beim Scouting von Torhütern eingesetzt werden. Dazu wird die erwartete Anzahl an Gegentoren durch die Summe der Trefferwahrscheinlichkeiten aller Torschüsse gegen einen Torwart berechnet und mit der tatsächlichen Anzahl an Gegentoren verglichen. Dies stellt einen wesentlich besseren Indikator zur Leistung eines Torwarts dar als die Anzahl an Gegentoren oder der Anteil an parierten Schüssen. Die Gegentoranzahl hängt nämlich neben der Torwartleistung auch in starkem Maße von der Leistung der Defensive und der gesamten Mannschaft ab, sodass Torhüter von schwächeren Mannschaften deutlich mehr Schüsse aufs Tor bekommen als Torhüter von stärkeren Mannschaften. Die Prozentzahl der gehaltenen Torschüsse bezieht zwar die Quantität der Torschüsse mit ein, aber nicht die Qualität dieser Torschüsse. Das Expected Goals Modell enthält dagegen sowohl die Quantität als auch die Qualität der Torschüsse und bewertet so die Leistung eines Torwarts unabhängig von der Mannschaft, in der ein Torwart spielt. Die folgende Tabelle zeigt beispielsweise die Anzahl an erwarteten und tatsächlichen Gegentoren von Torhütern, für die das Expected Goals Modell mindestens fünf Gegentore bei der WM 2018 prädiktierte und deren tatsächliche Anzahl an Gegentreffern geringer ist als die erwartete Anzahl an Gegentoren. Dabei fallen gleich vier Torhüter auf, die über die Hälfte der erwarteten Gegentore verhindern konnten. Beispielsweise ließ Kasper Schmeichel bei dem Turnier nur zwei Gegentreffer zu, obwohl das Expected Goals Modell 7,4 Gegentore für Dänemark erwartete.

Bewertung von Mannschaftsleistungen

Des Weiteren kann das Expected Goals Modell auch zur Einordnung von Mannschaftsleistungen genutzt werden. Dazu können die Ergebnisse von Spielen durch die Anwendung des Expected Goals Modell auf alle Torschüsse in den jeweiligen Spielen prädiktiert werden. So kann geprüft werden, welche Mannschaften im Vergleich zum Expected Goals Modell besser oder schlechter abschneiden. Die Ergebnisse nach dem Expected Goals Modell sind dabei häufig ein besserer Indikator für zukünftige Ergebnisse als die wirklichen Ergebnisse, da sie nicht so anfällig für das Spielglück der einen oder anderen Mannschaft sind und damit weniger vom Zufall abhängen. Dies kann von Fans als Wettstrategie eingesetzt werden und Trainern als Hinweis dienen, ob die Ergebnisse der eigenen Mannschaft mit der Leistung übereinstimmen.

Eine weitere Möglichkeit für die Anwendung des Expected Goals Modells stellen Race Charts dar. Diese beschreiben den Verlauf eines Spiels ziemlich genau, indem sie die Trefferwahrscheinlichkeit für jeden Torschuss einer Mannschaft kumuliert abbilden. So zeigt die untenstehende Abbildung den Expected Goals Race Chart zum Champions League Finale 2005 zwischen dem AC Mailand und dem FC Liverpool.

Dabei ist erkennbar, dass der Favorit aus Mailand bereits mit dem ersten Torschuss durch Paolo Maldini in Führung ging. Anschließend war das Chancenverhältnis in den ersten 35 Minuten jedoch ausgeglichen, bis Hernán Crespo per Doppelpack kurz vor der Halbzeit auf 3:0 für den AC Mailand stellte. Das Expected Goals Modell prädiktierte bis zur Halbzeit hingegen nur 1,17 Tore für Milan und 0,18 Tore für Liverpool, was dafürspricht, dass Milan seine Torchancen in der ersten Halbzeit äußerst effizient verwertete. Dies änderte sich jedoch im weiteren Spielverlauf, während Liverpool mit zwei unwahrscheinlichen Toren durch einen schwierigen Kopfball von Steven Gerrard und einen Fernschuss von Vladimir Smicer auf 3:2 herankam. Kurz darauf verwandelte Xabi Alonso einen Elfmeter im Nachschuss zum Ausgleich. Im Anschluss an den Ausgleich hatte Liverpool kaum noch gefährliche Torabschlüsse, während die Italiener sowohl in der restlichen regulären Spielzeit als auch in der Verlängerung zahlreiche Gelegenheit vergaben, um erneut in Führung zu gehen. Eine besonders hohe Trefferwahrscheinlichkeit hatte dabei der Schuss von Andriy Shevchenko in der 117. Minute, wobei Jerzy Dudek durch eine Weltklasseparade den Siegtreffer für Milan kurz vor Ablauf der Verlängerung verhinderte. Somit endete das Spiel 3:3 nach Verlängerung und Liverpool gewann das Finale im Elfmeterschießen. Nach dem Expected Goals Modell wäre der wahrscheinlichste Ausgang des Spiels ein 2:2 nach 90 Minuten und ein 3:2 Sieg für den AC Mailand nach der Verlängerung gewesen.

Insgesamt bietet ein solcher Race Chart einen guten Überblick zu dem Spielverlauf sowie dem Chancenverhältnis zwischen den beiden Mannschaften. Daraus lässt sich zum Beispiel ableiten, welche Mannschaft in bestimmten Phasen des Spiels torgefährlicher war. So beschreibt der Race Chart die Leistung der beiden Mannschaften genauer als das reine Ergebnis und bietet daher auch einen besseren Indikator für die Siegwahrscheinlichkeit einer Mannschaft in den nächsten Spielen. Diese zusätzlichen Informationen können zum Beispiel in Krisenzeiten von Klubverantwortlichen bei der Entscheidung genutzt werden, ob ein Trainerwechsel zum aktuellen Zeitpunkt sinnvoll ist. Durch die Unterscheidung zwischen einer Ergebniskrise und einer Leistungskrise können somit rationalere Entscheidungen getroffen werden, die weniger stark von der aus den letzten Ergebnissen resultierenden Emotionalität beeinflusst werden. Dies kann einen unnötigen und kostspieligen Trainerwechsel verhindern oder im Falle von glücklichen Punktgewinnen zu einer rechtzeitigen Reaktion von Trainern oder Klubverantwortlichen führen, bevor die Ergebnisse durch schwindendes Glück schlechter werden.

Fazit zu expected Goal Modell

Die Entwicklung eines Expected Goals Modells als neuronales Netz bietet einen interessanten Einblick, welche Parameter die Trefferwahrscheinlichkeit eines Torschusses positiv oder negativ beeinflussen. Zudem ergeben sich durch das Modell vielfältige Einsatzmöglichkeiten zum Spielerscouting und zur Bewertung von Mannschaftsleistungen. Somit ist das Expected Goals Modell ein Beispiel für das Potenzial von Data Science und Machine Learning im Fußball oder anderen Sportarten, welches noch längst nicht ausgeschöpft ist. Schaut auch in unserem Impuls zur Spielanalyse in Python vorbei.

Sie möchten mehr über die Möglichkeiten von Data Science erfahren? Dann nichts wie ab zu unserem Data Strategy & Analytics Assessment!

Übersicht der Data Science (ML & AI) Serie:

• • • AI im Fußball: Entwicklung eines Expected Goals Modells
    • Einführung in Deep Learning und PyTorch
    • NLP zur Analyse von E-Mails
    • Entwicklung eines Machine Learning Modells auf Azure
    • Architektur und Funktionsweise von neuronalen Netzen
    • Entwicklung eines neuronalen Netzes zur Prädiktion von Airbnb-Preisen
    • Architektur und Funktionsweise von baumartigen Regressionsverfahren
    • Entwicklung baumartiger Regressionsverfahren zur Prädiktion von Airbnb-Preisen
    • Was sind Large Language Modelle
    • Das Large Language Model GPT-4
    • Prompt Engineering in ChatGPT
    • Entwicklung eines Large Language Modells mit LangChain & OpenAI
    • Überblick zu Künstlicher Intelligenz, Machine Learning und Deep Learning
    • Maschinelles Lernen in Databricks mithilfe von MLlib

Haben wir Ihr Interesse geweckt? Kontaktieren Sie uns!

Ihr Ansprechpartner

Christoph Espelage

christoph.espelage@datalytics-consulting.com

+49 178 3984086