Serie | Data Science (ML & AI) – Architektur und Funktionsweise von neuronalen Netzen

Architektur und Funktionsweise von neuronalen Netzen

Neuronale Netze bestehen aus mehreren Schichten von miteinander verbundenen Neuronen zur Simulation des menschlichen Gehirns. Im Gegensatz zu traditionellen Machine Learning Algorithmen, wie Linearer Regression, profitieren neuronale Netze durch die Vielzahl an Parametern von einer enormen Menge an Trainingsdaten. Neuronale Netze eignen sich beispielsweise zur

• Klassifikation von Bildern,
• Spracherkennung oder für
• personalisierte Produktempfehlungen.

Aufbau eines Perzeptrons

Das Perzeptron ist die einfachste Architektur eines Artificial Neural Networks, welches 1957 von Frank Rosenblatt erfunden wurde. Das künstliche Neuron, welches auch threshold logic unit (TLU) genannt wird, berechnet eine gewichtete Summe der Input-Werte und wendet dann eine Aktivierungsfunktion bzw. Treppenfunktion an. Jedem Input-Wert wird dabei ein Koeffizient zur Ermittlung der gewichteten Summe zugewiesen. Zudem wird der Summe noch ein Bias-Wert hinzugefügt. Insgesamt ergibt sich somit als Output-Wert des Perzeptrons:

h_w(x) = step(x^Tw + b) = step(w₁x₁ + w₂x₂ + … + w_nx_n + b)

Als Treppenfunktion wird beim Perzeptron meistens die Heaviside-Funktion verwendet, welche für negative Zahlen 0 und sonst 1 ist.

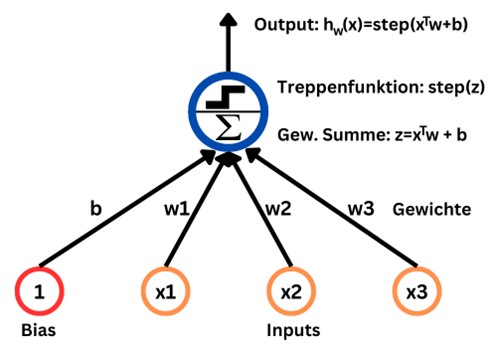
Beim Training des Perzeptrons geht es darum, die Gewichte so zu optimieren, dass der prädiktierte Output möglichst nah am tatsächlichen Wert liegt.

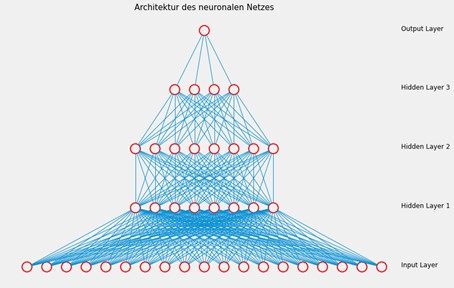
Architektur eines neuronalen Netzes

Ein neuronales Netz hat die Struktur eines Graphen mit Knoten und Kanten. Die Knoten werden als Neuronen bezeichnet und repräsentieren eine Recheneinheit, welche den Wert einer Funktion f(x) basierend auf allen Input-Werten berechnet. Die Funktion f(x) könnte beispielsweise alle Input-Werte aus dem Vektor x aufsummieren und die Summe als Output zurückgeben. Die Kanten verbinden ein Neuron aus einer Schicht mit einem anderen Neuron aus der nächsten Schicht. Jede Kante übergibt dabei neben dem Output des ursprünglichen Neurons auch einen Multiplikationskoeffizienten an das nächste Neuron, sodass dieses Neuron eine gewichtete Summe der Input-Werte berechnen kann.

Ein neuronales Netz setzt sich zusammen aus einer

• Input Layer,
• beliebig vielen Hidden Layers und
• einer Output Layer.

Die Input Layer definiert die Features des Modells und nimmt entsprechend die Input-Werte dieser Features entgegen. Daher enthält die Input Layer für jedes Feature genau ein Neuron. In den Hidden Layers finden die Berechnungen statt, um auf Basis der Input-Werte Vorhersagen zu treffen. Die Anzahl der Hidden Layers und die Anzahl der Neuronen in den einzelnen Hidden Layers sind beliebig und müssen vom Entwickler als Hyperparameter festgelegt bzw. optimiert werden. Die Output Layer liefert schließlich das Ergebnis des neuronalen Netzes, wobei die Anzahl der Neuronen in der Output Layer der Anzahl der zu prädiktierenden Werten entspricht.

Wie lernen neuronale Netze?

Beim Training eines neuronalen Netzes geht es darum, die Gewichte der Koeffizienten einzustellen. Je mehr Kanten es gibt, desto mehr Parameter muss das Modell lernen. Zum Lernen werden Trainingsdaten mit (x, y) Wertepaaren benötigt, wobei x den Input-Vektor mit den Werten für die einzelnen Features beschreibt und y die Zielvariable(n) enthält. Während des Trainings passt das neuronale Netz die Gewichte der Kanten so an, dass die Output-Neuronen möglichst ähnliche Werte zu y generieren, wenn x als Eingabewerte an die Input Layer übergeben wird.

Diese Anpassung der Gewichte wird durch Backpropagation erreicht. Dazu wird für jedes Trainingsbeispiel der Fehler berechnet, welcher sich aus der Abweichung zwischen dem vom Modell prädiktierten Wert und dem tatsächlichen Wert ergibt. Die Methode zur Berechnung des Fehlers wird als Kostenfunktion bezeichnet und könnte beispielsweise die quadrierte Differenz zwischen dem prädiktierten und tatsächlichen Wert sein. Anschließend werden die Gewichtskoeffizienten so verändert, dass die Kostenfunktion minimiert wird. Bei der Backpropagation wird der Fehler zunächst an die letzte Hidden Layer übergeben, um dort die Gewichte zu verändern. Danach erfolgt die Anpassung der Gewichte in der vorletzten Hidden Layer, indem die Parameter so gewählt werden, dass die Ergebnisse aus dieser Schicht mit den darauf angewendeten Berechnungen der letzten Hidden Layer einen möglichst geringen Fehler produzieren. Somit erzeugt das neuronale Netz durch eine Forwardpropagation von der Input Layer zur Output Layer Vorhersagen und beim Training lernt das neuronale Netz die richtige Einstellung der Parameter dadurch, dass der Fehler bei der Backpropagation in der entgegengesetzten Richtung zurückgegeben wird.

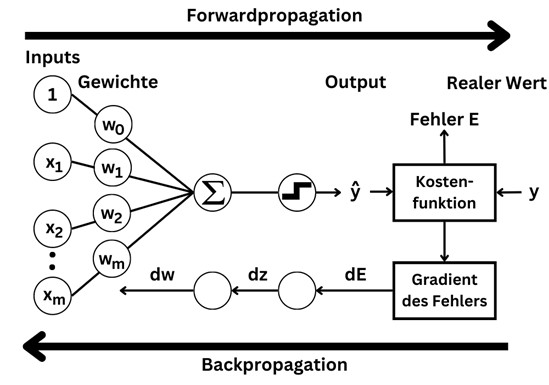
Die Anpassung der Gewichte erfolgt durch Gradient Decent, wobei der Gradient der Kostenfunktion vom Modell in Bezug auf jeden einzelnen Parameter des neuronalen Netzes berechnet wird. Nach der Ermittlung des Gradienten werden die Parameter durch einen Gradient Decent Schritt angepasst. Dieser Prozess wird so lange wiederholt, bis das neuronale Netz zur Lösung konvergiert.

Hyperparameter

Die Werte für Hyperparameter müssen vor dem Training eines Modells festgelegt werden und bleiben während des Trainings konstant. Beispiele für Hyperparameter von neuronalen Netzen sind die

• Lernrate,
• Batchgröße und
• Menge an Epochen sowie die
• Anzahl an Hidden Layers und die
• Anzahl deren Neuronen.

Bei der Wahl der Anzahl an Hidden Layers und deren Neuronen geht es darum, das neuronale Netz mit einer ausreichenden Größe zu gestalten, um möglichst genaue Vorhersagen zu erhalten. Allerdings können zu viele Neuronen zu einem Overfitting führen, sodass sich das neuronale Netz zu stark an die Trainingsdaten anpasst und eine schlechtere Generalisierung auf neuen Daten erreicht. Außerdem steigt mit der Anzahl an Neuronen auch die Komplexität und Rechenzeit zum Training des Modells. Dementsprechend ist die Anzahl der Schichten und Neuronen entscheidend für die Definierung der Architektur eines neuronalen Netzes.

Der wahrscheinlich wichtigste Hyperparameter ist die Lernrate, mit welcher festgelegt wird, wie stark die Gewichte bei der Backpropagation angepasst werden. Je höher die Lernrate gesetzt wird, desto größere Schritte werden beim Gradient Decent ausgeführt. Eine hohe Lernrate führt somit zu einer schnelleren Konvergenz beim Training, was jedoch in einer suboptimalen Lösung resultieren kann. Bei einer kleinen Lernrate werden dagegen mehr Epochen zum Training des Modells benötigt, da bei jedem Durchlauf nur leichte Veränderungen an den Gewichten vorgenommen werden.

Eine Epoche beschreibt einen Durchlauf des Trainingszyklus, in dem das neuronale Netz auf dem gesamten Trainingssatz trainiert wird. Dabei läuft jede Zeile des Trainingssatzes genau einmal per Forwardpropagation und Backpropagation durch das neuronale Netz. Eine Epoche kann aus einem oder mehreren Batches bestehen. Bei einer Batchgröße von 50 wird der Trainingssatz beispielsweise in disjunkte Teile mit jeweils 50 Zeilen aufgeteilt, welche dann gleichzeitig das neuronale Netz durchlaufen. Auf Basis des jeweiligen Batches wird dann der durchschnittliche Fehler berechnet, der bei der Backpropagation zur Anpassung der Gewichte verwendet wird. Nachdem alle Batches des Datensatzes zum Training des Modells genutzt wurden, endet eine Epoche und der Trainingsprozess wird mit Beginn der nächsten Epoche fortgeführt, bis die Anzahl der zuvor festgelegten Epochen absolviert wurden.

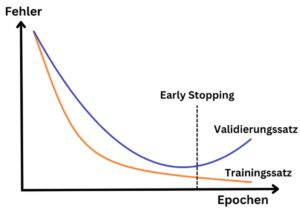
Die Schwierigkeit bei der Wahl der Anzahl an Epochen liegt darin, dass bei zu wenigen Epochen keine Konvergenz der Kostenfunktion erzielt wird, während zu viele Epochen zu Overfitting führen können und gleichzeitig den benötigten Rechenaufwand erhöhen. Daher stellt Early Stopping eine alternative Methode zur Beendigung des Trainings dar. Hierbei wird nach jeder Epoche der Fehler des Modells auf dem Validierungssatz mithilfe der Kostenfunktion ausgewertet. Sobald dieser Fehler beginnt zu steigen, wird das Training abgebrochen, auch wenn zu diesem Zeitpunkt noch nicht die gewählte Anzahl an Epochen abgeschlossen wurden. So kann die Anzahl der Epochen zu Beginn hoch angesetzt werden, um eine Minimierung der Kostenfunktion sicherzustellen und gleichzeitig mit Early Stopping ein Overfitting des neuronalen Netzes zu vermeiden.

Zusätzlich muss auch die Aktivierungsfunktion für die einzelnen Schichten bestimmt werden. Die Aktivierungsfunktion definiert, wie die Treppenfunktion beim Perzeptron, die Transformation der gewichteten Summe in einen Output des jeweiligen Neurons. Die Wahl der Aktivierungsfunktion in der Output Layer ist abhängig von der Art des Prädiktionsproblems. Bei einem Regressionsproblem sollte

• eine lineare Aktivierungsfunktion gewählt werden.

Für die Lösung eines Klassifikationsproblems empfiehlt sich die Nutzung von

• Sigmoid für eine binäre Klassifikation,
• Softmax für eine Multi-Klassen-Klassifikation und
• Sigmoid für eine Multi-Label-Klassifikation.

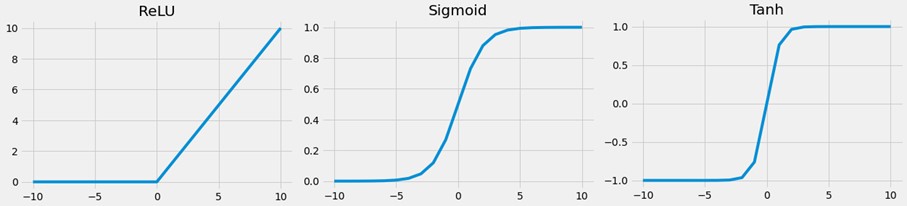
Die Festlegung der Aktivierungsfunktionen in den Hidden Layers beeinflusst das Lernverhalten des neuronalen Netzes. Hier werden typischerweise differenzierbare, nichtlineare Aktivierungsfunktionen verwendet, sodass das Modell auch nichtlineare Zusammenhänge leichter lernt. Die am häufigsten genutzten Aktivierungsfunktionen in Hidden Layers sind

• Rectified Linear Activiation (ReLu),
• Sigmoid und
• Tanh.

In der Regel wird dabei für jede Hidden Layer eines neuronalen Netzes die gleiche Aktivierungsfunktion verwendet.

Als Kostenfunktion wird für Regressionsprobleme meistens

• Mean Squared Error,
• Mean Absolute Error oder
• Huber genutzt.

Der Mean Squared Error berechnet die quadrierte Differenz zwischen dem prädiktierten und tatsächlichen Wert, sodass diese Metrik stark von Ausreißern beeinflusst wird. Wenn der Datensatz viele Ausreißer enthält, wird häufig stattdessen der Mean Absolute Error bevorzugt, welcher durch die Berechnung der absoluten Differenz weniger anfällig für Ausreißer ist. Eine Kombination dieser beiden Metriken stellt Huber dar, wobei hier der Mean Squared Error verwendet wird, wenn die Differenz unter einen bestimmten Schwellwert liegt, und über diesem Schwellwert wird der Mean Absolute Error genutzt. Dadurch ist Huber robuster gegenüber Ausreißern als der Mean Squared Error, während der quadratische Teil dennoch zu einer schnelleren Konvergenz führt als der Mean Absolute Error.

Fazit zu neuronalen Netzen

Neuronale Netze bestehen aus mehreren Schichten mit einer

• Input Layer,
• beliebig vielen Hidden Layers und
• einer Output Layer.

Diese Schichten können unterschiedlich viele Neuronen besitzen, welche durch gewichtete Kanten miteinander verbunden sind. Das Ziel beim Training eines neuronalen Netzes besteht darin, diese Gewichte so anzupassen, dass die Abweichung zwischen den vom Modell prädiktierten Werten und den tatsächlichen Werten möglichst gering wird.

Nach der Vorstellung der Funktionsweise von neuronalen Netzen geht es im nächsten Teil um die praktische Anwendung von neuronalen Netzen, indem ein Modell zur Prädiktion von Airbnb-Preisen entwickelt wird.

Sie möchten mehr über die Möglichkeiten von Data Science erfahren? Dann nichts wie ab zu unserem Data Strategy & Analytics Assessment!

Übersicht der Data Science (ML & AI) Serie:

• AI im Fußball: Entwicklung eines Expected Goals Modells
• Einführung in Deep Learning und PyTorch
• NLP zur Analyse von E-Mails
• Entwicklung eines Machine Learning Modells auf Azure
• Architektur und Funktionsweise von neuronalen Netzen
• Entwicklung eines neuronalen Netzes zur Prädiktion von Airbnb-Preisen
• Architektur und Funktionsweise von baumartigen Regressionsverfahren
• Entwicklung baumartiger Regressionsverfahren zur Prädiktion von Airbnb-Preisen
• Was sind Large Language Modelle
• Das Large Language Model GPT-4
• Prompt Engineering in ChatGPT
• Entwicklung eines Large Language Modells mit LangChain & OpenAI
• Überblick zu Künstlicher Intelligenz, Machine Learning und Deep Learning
• Maschinelles Lernen in Databricks mithilfe von MLlib

Haben wir Ihr Interesse geweckt? Kontaktieren Sie uns!

Ihr Ansprechpartner

Christoph Espelage

christoph.espelage@datalytics-consulting.com

+49 178 3984086